How to recharge a Nikon Coolpix P310

I'm just putting this out there in the hopes that one day someone else will stumble across this and I'll save them some time and head-scratching caused by a bone-headed design decision.

The Nikon Coolpix P310 is a lovely camera, it has great picture quality, fantastic performance in low-light conditions, it's small, rugged, light, and it has great optics. It just has one very annoying design flaw, you can't recharge it from an ordinary USB port.

It comes with a proprietary connection cable, it's USB at one end and something unique at the other end where it plugs in to the camera. I have no idea why they didn't go with mini-USB or micro-USB like, oh I don't know, every other digital camera in existence, but whatever, it'll just really suck to lose it.

Anyway, this one cable is both the data link and the recharging cable, which is why it needs to be USB at one end, so that it can plug in to your computer. The problem is that nowadays a lot of devices recharge using a USB cable, so we've come to expect that if there's a rechargeable device with a USB plug on one end it means we can plug it into a standard 5V 0.5A USB charger and it'll charge-up just fine, if perhaps a bit more slowly than normal. Apple iDevice owners are now covering their mouths with their hands and sniggering at me, but the rest of you are probably nodding along and thinking this is an entirely reasonable notion.

The Nikon Coolpix P310 does not recharge from a standard charger. You must use their proprietary charger before the camera will draw any power whatsoever. It won't even draw power from your computer when you've connected it to download your pictures.

So if you're going-away for a while, not only do you have to cart-around their strange cable, you also have to take their wall charger with you too because that other charger you're taking with you for all your other devices won't work.

Portable phone charger

Hello! Been a while, hasn't it? Sorry about that, but I'm back now. The piano synth articles will continue soonish, I've been having lots of fun getting my old code working in new environments, and I should be able to write it all up soon.

Meanwhile...

I've been playing a fair bit of Ingress lately. It's an alternate-reality game, meaning you have to get off your behind and travel around to places in the real world in order to play the game. Good for exercise, but the problem is that even on my Nexus 4 with its lovely amounts of battery life the game burns through power at a staggering rate, from fully-charged to flat after only 2-3 hours of continuous play.

So I thought it might be worth buying a portable battery charger, essentially a high-capacity LiPo battery with a USB-compatible output. Then I looked at the price of them. Not cheap, not really an impulse purchase.

I estimated that the bulk of the cost would be in the battery itself, and I already have some high-capacity rechargeable LiPos floating-about in the form of RC airplane batteries. Perhaps I could do something with them? It turns out I can!

My RC plane batteries happen to be 12 volts or thereabouts (for the curious, they're 3S - meaning 3 x 3.7V cells in series), which is the same voltage that car cigarette lighter sockets provide. So, if I can hook-up an RC plane battery to a lighter socket, then in theory I can use a car cellphone charger to recharge my phone on the go.

Here are all the parts laid-out:

1. 1800mAh 3S 11.1V LiPo RC plane battery. I already possess a few of these so I didn't pay anything, but a new one is around $12.50 at the moment. 
2. Flexible electrical wire. I chose 14 AWG just because I had some already and it matches the battery's wire, though I don't actually need that gauge, not at the discharge rates we'll be dealing with. I probably used about $0.50 worth of wire, at a guess.
3. A car cigarette lighter socket. Cost: $1.50.
4. A male Deans connector. I use Deans connectors for all my RC batteries so I just need a male plug to connect to the battery. The real thing comes in packs of two for about $3.50, but you can also find bulk packs of cheap knock-offs for much less.
5. A car cellphone charger. This one cost me $5.80, a real bargain!
6. Heat-shrink tubing. I'm not even going to bother pricing this one, for the amount I used it's less than a cent.

Total cost, somewhere in the region of $10, plus $12.50 for a new battery.

Here's how it all goes together, step by step.

Step 1: Solder the two wires to the terminals of the socket. The positive terminal is the centre pin, while the negative is the outer wall. Following convention, I used red for positive and black for negative. I'm not brilliant at soldering, but it does the job.

Step 2: Tie a knot in the wires and slip the end cap on. The knot is there so that if the wire is pulled too roughly it won't damage the solder joints.   

Step 3: Screw the end cap onto the socket, and then use some heat-shrink tubing to protect the place where the wires come out.

Step 4: Cut the wire to a sensible length - I chose around six inches - and then solder the Deans connector to the other end.

Note: don't forget to slide your heat-shrink tubing onto the wires BEFORE you do this, otherwise you'll have to desolder them and do the whole thing again and feel like an idiot. I speak from experience ;-)

Using a hairdryer to shrink the tubing onto the solder joints:

And that's pretty much all there is to it! Here's the whole thing connected-together and charging my phone. I switched-off the flash for this shot so you can see the pretty blue glow from the charger:

A close-up on the phone screen, to show it's really charging:

And that's how I spent my evening.

Going further, I have a low-voltage alarm on its way to me from somewhere in China, which attaches to that spare white connecter dangling from the battery. The reason for this is that LiPo batteries really hate being discharged all the way, it pretty much just bricks them, so you always want to leave some charge in them even when they're "empty". I'll program the alarm with a safe minimum voltage and it buzzes when the battery gets down to that point, reminding me to disconnect. It also has a cute LED readout to display the current voltage so I can see at a glance how it's going. 

The batteries I use are 1800mAh, which is a measure of how much charge they store. If I want to carry more weight and spend more money I can go up to larger batteries, 5000mAh and beyond. But I prefer these because their main use is flying planes where weight is important.

My phone has a 2100mAh internal battery but that's only 3.7V, so because the RC plane battery is 3 times the voltage it's actually equivalent to about 5400mAh at 3.7V, or another 2.5 full charges. As I already stated I can't use all of that power, some needs to remain in the battery to avoid damage. I don't yet know how much that will be, so I'm going to have to wait until I have the alarm to know how much charge I can get out of it. 

My colleague Ken who knows far more than I do about phone chargers, has suggested that this kind of switching power supply is about 80% efficient at converting electricity from 12V down to the 5V the phone needs, and so I expect I'll actually see about 1 to 1.5 full phone charges from a single fully-charged RC plane battery, which ought to give me up to about 6 hours' autonomy in Ingress before I have to go home to recharge, or about 9 hours if I carry two batteries with me.

Of course, my family might have something rude to say about it if I decide to spend all day out playing video games...

It's been more than three years since I last wrote anything here. I left you dangling with the piano synthesizer articles and then disappeared. I apologize.

Shortly after writing my last article I moved to Canada to work for Electronic Arts, initially as an audio programmer and then in other roles. I didn't really have the time or motivation to work on the articles any more, especially with EA's somewhat draconian-worded non-compete clause; and so I let the blog fall into disuse.

I did however leave behind a small stat counter embedded in the site so that I could see how many people come to visit. The results are interesting, I was expecting it to be pretty much 100% web crawlers by now but I'm still seeing many visitors who search Google for things related to the way a piano sounds, and they land on my site.

On the whole, I'm seeing about three unique visitors per day. It's hardly Reddit or BoingBoing I've got going on here but the discovery has been enough to nudge me back into thinking about finishing the piano synth articles, and then going-on and writing about other things related to audio programming.

The second nudge came from my recent job change to another games company in Canada, one whose non-compete clause is a lot more forgiving on the things they "allow" me to do on my own time with my own equipment.

The eagle-eyed among you will also notice a change to my user profile, specifically my name. Alex Lennox was a made-up name, intended to keep me anonymous from my employer. I've decided that since I don't plan to post anything here other than informative articles, I might as well use my own name instead.

So, in short: happy new year everyone, and watch this space!

Piano 3 - Towards the piano sound

You can have the smallest music in the world, all compressed down into mere bytes, but if the instrument playing it sounds rubbish then what’s the point? We need a virtual Pianola, a (small) piece of code that responds to commands and makes a noise like a piano should. We need a piano synthesizer.

First things first, what does a piano actually sound like? You can’t just grab any old piece of piano music and listen to it; you need to have a clean controlled recording of the piano playing a single note, otherwise you can’t analyse it properly. Preferably, you’ll have a whole set of these recordings covering the range of piano notes, with each note recorded at a few different velocities (the velocity is how hard you hit the piano key).

Luckily for me, I don’t need to go out with a microphone and find a grand piano to take recordings from, because other people have already done exactly that. SoundFont files are the result, a bank of recordings of an instrument playing a range of notes at a range of velocities. Most SoundFonts are expensive to buy, but I located two high quality examples online which are free to download. Extracting the notes from a SoundFont is easy, and you end up with a few dozen sound files like this one:

Piano note A3 forte

The first thing you notice when you listen to them all is that the notes all sound different to each other. Not just higher and lower pitched versions of each other, but qualitatively different. If for instance you take a middle C4 note and pitch-shift it down by two octaves, you do not arrive at an acceptable sounding C2 note. It will sound too thin and plinky. The lower notes on a piano have a deep sonorous bell-like quality to them that the higher notes do not have.

The second thing you notice is that even the different velocities sound different to each other; they are not just louder and quieter. The harder you hit a note the brighter it sounds, and when you study it with the help of a sound analysis program, you see that this is because the stronger note contains more powerful high-frequency components to it.

One of the most useful ways to study an audio signal is to treat it the same way as the human ear does. Your ear has thousands of tiny little hairs inside which are all different lengths, and they vibrate at different sound frequencies. When you hear a sound, each hair in your ear vibrates to a greater or lesser amount according to how much the sound contains its resonant frequency. If you hear a very pure tone, only a few of the hairs in your ear will vibrate. If you hear white noise, they’ll all be vibrating together. Your brain decodes all of this and turns it back into sound in your mind.

The computer equivalent of this process is called a Fourier transform, and when you run an audio signal through it, out will pop a neat graph of loudness versus frequency. This is what the piano note above looks like when you run it through a Fourier transform:

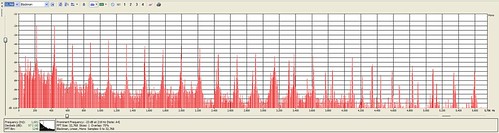
(click the image to download a larger version)

The note is A3, which has a frequency of 220Hz. The first thing you notice is that it is arranged into a series of spikes. The biggest spike on the left is the fundamental tone at 220Hz. The other spikes to the right of it are called overtones, and they give the piano note its character. In the musical world, the musical character from overtones is called timbre.

Something you may notice is that the overtones are evenly spaced, they are whole-number multiples of the fundamental frequency. Overtones like this are called harmonics. In fact a piano's overtones aren’t quite perfect harmonics, but they are close enough for government work. We don’t need to study the difference until the next article when we talk about physical modelling.

As we’ve already stated, the overtones provide character to the note, they give the musical instrument its voice. To illustrate this, listen to the note below which is simply a pure tone at 220Hz with no overtones, and compare it with the piano note from above.

Pure tone note A3

Quite a significant difference!

An idea strikes me around this time in the study. How about if, for each piano note, I simply store the height and frequency of the most important spikes in that graph? We could probably get away with recording about 20-30 spikes, and that would give us a reasonable reproduction of the piano’s timbre. Throw it through an inverse Fourier transform, and pull the audio signal out of the other side.

I don’t have a recording handy, but I can assure you that it sound's pretty good, a fairly reasonable piano-like sound. Unfortunately it has two critical drawbacks:

1. Those spikes decay at different rates on a real piano, the high frequency overtones decay faster than the lower frequencies. The result is a bright punchy start to the note, and a duller ringing tail-off. We’ve lost that, and it’s hard work to get it back.
2. The bass notes definitely do not sound good with only 30 overtones. They are so rich in overtones that we need at least 100! Imagine for each overtone that we want to store frequency (4 bytes) and power (another 4 bytes). That’s 800 bytes for one bass note at one velocity level. The piano has 88 notes, and we’re going to need several key velocities. It doesn’t scale-up well.
   

In the end, rebuilding a signal like this from overtones can be thought of as a very strange and unique form of lossy compression. As we learned in the previous article, data compression doesn’t work very well at getting us down to the required sizes needed for packing everything into a 64KB demo.

So we go back to the drawing board, in search of a more procedural solution.

Thankfully, brighter minds have been applying their considerable capabilities to the same problem for years, albeit for different reasons, and they have been achieving impressive results with a technique called physical modelling. Briefly, physical modelling is a way of simulating the actual inner workings of the piano, in order to arrive at a completely procedural synthesis of the sound.

In the next article we will explore some of the current approaches to physically modelling the piano, and then focus on the one I chose for the demo.

Piano 2 - Size is everything

In part 1 I talked briefly about storage space, about how compressing a music player and a piece of music into less than 64KB is an important problem to solve.

Let's say, for example, that the demo is going to be five minutes long. For high quality music we need to choose a nice high sample rate, so let's do the same as CD and choose 44,100 samples per second. Each sample is two bytes in size and the music is stereo, so we have a total of 176,400 bytes per second. Therefore, if we simply pre-record the music and store it we would have just about enough for one third of a second of music.

And that's if we completely fill the entire 64KB demo with only music; we still need to put the graphics in there somewhere too! This is not a very good start.

So the obvious choice is: compress it! There are lots of cool music compression algorithms out there, the most famous and popular is MP3. It's not the best but it's not far off, either. MP3 gives us the ability to trade quality for storage space by changing the encoding bit-rate. An acceptable quality bit-rate is around 128Kbit per second. There are eight bits in a byte, so that makes 16KB per second, giving our demo a maximum of about four seconds of music.

Compression isn't working for us, time for a re-think.

We need to start thinking about a more procedural approach to the problem. We don't actually need to record all of the music, we just need to know what notes to play and when, like a piano-roll zooming through a Pianola. If we can invent a small piece of code that makes a sound like a piano when we tell it to "play note X at time T", then our music can be much smaller, just a series of time-stamps and notes to play.

There are two common ways of doing this, MOD and MIDI. MOD was invented almost 20 years ago to represent the particular needs of the Amiga computer's sound chip. It is a very popular format for demo authors and its utility cannot be understated. However, in making a format that conforms to the needs of the Amiga, we find ourselves today fighting against its constraints. For example, the quietest non-silent volume level in a MOD file is -36dB, which doesn't give us very much in the way of dynamic range. It's fine for electronic music, and indeed many demo soundtracks are amazing works of electronica, but it's quite poor for playing classical music on a piano.

Another constraint is that you have to write the music in "patterns", almost like programming the music using subroutines. Again, this is fine for electronic music which tends to be structured on repetitive themes allowing a small number of patterns to be reused throughout the song, but it's much less useful for a classical piece which is constantly evolving.

So let's have a look at MIDI instead.

When you think of MIDI you're probably thinking of the cheesy music files you get all over the internet and in mobile phone ring tones. But this is not exactly the kind of MIDI I'm talking about. Those files are more accurately called General MIDI, and the reason why they sound naff is because the General MIDI system defines a certain set of instruments, and they are not normally well reproduced on PC soundcards.

What we're more interested in is the "old school" MIDI, which is nothing more than a simple stream of notes and other commands telling a musical instrument what to do. General MIDI at its heart is the same thing, but by stripping-away the extra General MIDI stuff that we aren't interested in, we arrive at a more compact representation of the music. But is it compact enough?

Let's see with an example. I chose the Moonlight Sonata by Beethoven, the full version in three parts which is a little over 15 minutes long. Downloading the General MIDI version off the internet, it weighs-in at 67KB. Trying to ZIP it will give us a reasonable idea of how it will compress in the final demo. Moonlight Sonata ZIPs down to 20KB. I can also strip-away the commands I'm not interested-in to see how that affects the file size, and the result is 65KB uncompressed, 18KB compressed.

That's really encouraging, finally we've found something that fits into 64KB, but we can do better. You see, the problem with MIDI is that it's one single sequence of commands. The note-on commands get jumbled together with the note-offs, tempo changes, sustain pedal on/offs, and so on. Compression algorithms such as ZIP don't enjoy this kind of heterogeneous melange; they prefer instead to have long homogeneous sequences of the same information repeating over and over.

For example if you have a song with a drum track which repeats over and over at exactly the same tempo for the entire song, ZIP compression can pack it down to into a small initial pattern, and then just say "...and repeat that 50 times". But if the other instruments are all mixed-together into the same stream, this is impossible.

So what we can do is to break-up our single MIDI sequence into a group of sequences, one for the note-on commands, one for the note-offs, and so on. This makes the data much more predictable, and thus easier to compress. It also makes the data smaller because we no longer need to name the command every time. In MIDI parlance, this is called "running status", and by splitting the commands out into separate streams we've effectively created the ultimate in running status.

Taking our Moonlight Sonata MIDI from earlier and doing this, we end up with a file that is somewhat smaller at 54KB, and it ZIPs down to 16KB.

That's a really good result for almost sixteen minutes of non-repetitive music!

Additionally, there is still plenty of room for experimentation to try and get the file size down even smaller. Depending on the music we eventually choose, we might have a very rhythmic set of bass notes, which could benefit from being broken-out into separate tracks. And the same goes for arpeggiated melodies. The goal is always to isolate repetitive patterns into separate streams to give the compression algorithm a better chance.

Another experiment is to have the note numbers stored as delta-values instead of absolute. What does this mean? Well, if for example we have a middle C major chord (C, E, G) then the MIDI note numbers are 60, 64, 67. Rather than storing these absolute values we can instead store the differences between the note numbers: 0, 4, 3. This is known as delta encoding. If the notes are frequently evenly spaced (e.g. lots of chords, arpeggios) then our delta-encoded notes form into very regular patterns, and are thus easier to compress.

Each command comes in two parts: the time when it should occur, followed by information about the command. Another experiment we can try is to split these two pieces of information into two separate streams of information. This will give us two homogeneous streams rather than one heterogeneous one, which ought to compress better.

None of these experiments are worth trying right now because the results will depend heavily upon the music we finally choose for the demo. So we will put them aside for the time being and remember them for later.

The end result isn't recognisably MIDI any more and the software we must write to handle all of these streams playing together will be larger and more complex than a simple MIDI sequencer, but we can address those issues later. The important thing is that we've found a way to make music fit into our 64KB demo without compromising on quality.

In the next article I'll start talking about one of the other key problems in writing this piano synthesizer: How do you make a convincing noise like a piano in such a small amount of space?

Piano 1 - A piano synthesizer

In this series of articles, I'm going to talk about how I wrote a piano synthesizer.

I chose this project for a few reasons. Firstly, my eventual aim is to write a 64K demo, and I'll be needing some music for it. I'm getting tired of hearing the same old FM synths and MOD-tracked music, and so I decided to try and create a "real" instrument, to make something that sounds a bit different to all the other demos out there.

Additionally, despite having a career as an audio programmer I'll be the first to admit that I've never been the world's foremost expert on Digital Signal Processing (DSP) and so I chose a project which would force me to learn more about it.

Demos have to run in realtime on ordinary PCs. That means drawing at least thirty frames (images) per second, and preferably more than sixty. Most of the processor time is going to be needed for the graphics, and so the music synthesizer must be capable of generating one frame of music in considerably less time than one frame. I am aiming to get it under 10%, leaving the other 90+% of the processing time available for graphics.

64KB is not much room. The entire demo, code and data, must fit into this tiny space. Even the music alone causes problems. For example, MP3s are quite well compressed, you may agree. You can fit about eleven full albums onto a single CD if you compress them with MP3. However that still means that the music takes up about one megabyte per minute. Obviously, something else is needed, and I'll go into detail about the solution I picked.

So briefly, there were three main goals for my piano synthesizer:

1. It must sound as realistic as possible.
2. It must run as quickly as possible.
3. The total size of the code and music must be as small as possible.

The posts that follow will be a kind of tidied-up development diary of the project as it progresses.